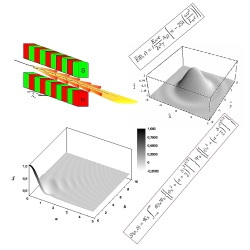
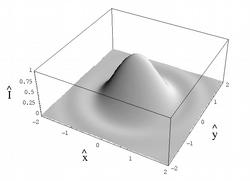
Figure 1: 3D plot of Eq. (1) in normalized units. For details about normalization please refer to the article
Gianluca Geloni,Evgeni Saldin,Evgeni Schneidmiller and Mikhail Yurkov
Deutsches Elektronen-Synchrotron (DESY), Hamburg, Germany
| Published as: | [3] G. Geloni, E. Saldin, E. Schneidmiller, M. Yurkov, Opt. Comm. 276, 1, p. 167 (2007) and [4] G. Geloni, E. Saldin, E. Schneidmiller, M. Yurkov, Nucl. Instr. and Methods in Phys. Res. A, 588, 3, 463(2008) |
In recent years, continuous evolution of synchrotron radiation (SR) sources has resulted in a dramatic increase of brilliance with respect to older designs. Among the most exciting properties of third generation facilities of today is a high flux of coherent X-rays [1]. The availability of intense coherent X-ray beams has triggered the development of a number of new experimental techniques based on coherence properties of light such as scattering of coherent X-ray radiation, X-ray photon correlation spectroscopy and phase contrast imaging. The interested reader may find an extensive reference list to these applications in [2].
Characterization of transverse coherence properties of SR at a specimen position is fundamental for properly planning, conducting and analyzing experiments involving above-mentioned techniques. These objectives can only be met once coherence properties of undulator sources are characterized and then propagated along the photon beamline up to the specimen.
Here we present a complete theory of spatial coherence for undulator radiation [3, 4]. First, we take advantage of Fourier Optics techniques to describe SR fields from a single electron in terms of a laser-like beam. Due to shot noise, electrons in the bunch have random offset, deflection and phase. Therefore, SR from an electron bunch is a random process that can be described as a incoherent superposition of many laser-like beams. Coherence properties are then quantified in terms of statistical correlation functions of the radiation field, providing simple semi-analytical expressions.
Our treatment constitutes the first comprehensive theory of coherence for SR from third generation light sources. Current estimations often assume that undulator sources are quasi-homogeneous, like thermal sources, and rely on the application of the van Cittert-Zernike theorem for calculating the degree of transverse coherence [2]. Such assumptions are not adequate when treating third generation facilities. Gaussian-Schell models [5, 6, 7], although interesting from a general theoretical standpoint, also turn out to be inadequate in the description of SR sources. For a detailed treatment we redirect the interested reader to [3, 4] and references therein.
Fourier Treatment of Near-Field Synchrotron Radiation Theory [ 3 ]
Fourier Optics (FO) [8] can be used to develop a formalism ideally suited for the analysis of any SR problem, including transverse coherence characterization, leading to establish basic foundations for the treatment of SR fields in terms of laser beam optics.
Using paraxial approximation, each polarization component of the slowly varying envelope of the electric field is represented in the space-frequency domain by a complex scalar function  , where
, where  are the coordinates of the observer. Radiation from an ultra-relativistic particle can be described as radiation from a virtual source, which produces a laser-like beam. The concept of virtual source has already been proposed (see [9], [10] and [11]). In this paper we develop the idea up to an analytical description of the laser-like beam. The virtual source itself is similar, in many aspects, to the waist of a laser beam, and often exhibits a plane wavefront. In this case it is completely specified, for any given polarization component, by a real-valued amplitude distribution of the field. The laser-like representation of SR is intimately connected with the ultra-relativistic nature of the electron beam: paraxial approximation applies and, therefore, free space basically acts as a spatial Fourier transformation. Thus, the field in the far zone (where the direction from any electron position to the observer can be considered constant along the trajectory) is, aside for a phase factor, the Fourier transform of the field at any position z down the beamline. It is also, aside for a phase factor, the Fourier transform of the virtual source.
are the coordinates of the observer. Radiation from an ultra-relativistic particle can be described as radiation from a virtual source, which produces a laser-like beam. The concept of virtual source has already been proposed (see [9], [10] and [11]). In this paper we develop the idea up to an analytical description of the laser-like beam. The virtual source itself is similar, in many aspects, to the waist of a laser beam, and often exhibits a plane wavefront. In this case it is completely specified, for any given polarization component, by a real-valued amplitude distribution of the field. The laser-like representation of SR is intimately connected with the ultra-relativistic nature of the electron beam: paraxial approximation applies and, therefore, free space basically acts as a spatial Fourier transformation. Thus, the field in the far zone (where the direction from any electron position to the observer can be considered constant along the trajectory) is, aside for a phase factor, the Fourier transform of the field at any position z down the beamline. It is also, aside for a phase factor, the Fourier transform of the virtual source.
Once the field at the virtual source is known, the field at other longitudinal positions, both in the far and in the near zone, up to distances to the sources comparable with the radiation wavelength, can be obtained with the help of the Fresnel propagation formula. This is possible due to the use of the space-frequency domain and the exploitation of the paraxial approximation. On the one hand, the Fresnel formula can be used to recover the field up to longitudinal positions which are further than a wavelength away from the sources. On the other hand, due to the paraxial approximation, the wavelength of interest in SR emission is very short compared with the radiation formation length and with the linear dimensions of the magnetic setup. Thus, the far-zone field completely specifies, through the Fresnel integral, the near-zone field as well. In the case when the electron generating the field is not ultra-relativistic, though, the paraxial approximation cannot be applied. As a result, the radiation wavelength is comparable with the radiation formation length. It is then impossible to reconstruct the near-field distribution from the knowledge of the far-field pattern.
An arbitrary number of magnetic devices is equivalent to several virtual sources and can be modelled as a sequence of appropriately chosen sources inserted between the edges of each magnetic structure. The use of virtual sources provides conceptual insight regarding SR sources and should facilitate their design and analysis. To give an example of the applicability of our method we treat the case of undulator radiation. Working within the applicability region of the resonance approximation the field at the virtual source, located in the middle of the undulator, is given by

and is shown in Fig. 1. Here Lw is the undulator length, K the undulator parameter, (−e) the electron charge, AJJ a coupling factor depending on K. Eq. (1) is found with the help of the far-zone field distribution and is propagated to any distance of interest. Effects due to a given particle offset and deflection with respect to the optical axis are also accounted for. This constitutes a startup point to investigate transverse coherence properties of third generation light sources.
Transverse coherence properties of X-ray beams in third-generation synchrotron radiation sources [ 4 ]
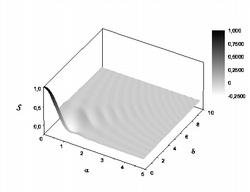
Figure 2: Plot of the universal function S, used to calculate the cross-spectral density at the virtual source.
This paper is mainly dedicated to a description of transverse coherence properties of SR sources. Therefore, it constitutes the first step for tracking coherence properties through optical elements, which can be only done when the source is quantitatively described. Solution of the problem of evolution of radiation properties in free-space is also given.
Since SR is a random process, the description of transverse coherence properties of the source and its evolution should be treated in terms of probabilistic statements. Statistical optics [12, 13] presents most convenient tools to deal with fluctuating electromagnetic fields. However, it was mainly developed in connection with polarized thermal light that is characterized by quite specific properties. Besides obeying Gaussian statistics, polarized thermal light has two other specific characteristics allowing for major simplifications of the theory: stationarity and homogeneity (i.e. perfect incoherence) of the source.
SR obeys Gaussian statistics, but stationarity and homogeneity do not belong to SR fields. Thus, although the language of statistical optics must be used to describe SR sources, one should avoid a-priori introduction of an incorrect model. In contrast to this, up to now it has been a widespread practice to assume that undulator sources are perfectly incoherent (homogeneous) and to draw conclusions about transverse coherence properties of undulator light based on these assumptions.
In particular, in the case of thermal light, transverse coherence properties of the radiation can be found with the help of the well-known van Citter-Zernike (VCZ) theorem [12, 13]. However, for third generation light sources either planned or in operation, the electron beam (geometrical) emittance is such that the VCZ theorem cannot be applied in the vertical direction, aside for the hard X-ray limit at wavelengths shorter than 0.1 Å. Similar remarks hold for future sources, like Energy Recovery Linac (ERL)-based spontaneous radiators.
Studying spatial-coherence properties of undulator sources is not a trivial task. Difficulties arise when one tries to simultaneously include the effect of intrinsic divergence of undulator radiation, and of electron beam size and divergence.
A model to describe partially-coherent sources, the Gaussian-Schell model, is widely used in statistical optics [5, 6, 7]. The Gaussian-Schell model includes non-homogeneous sources, because the typical transverse dimension of the source can be comparable or smaller than the transverse coherence length. However it does not provide a satisfactory approximation of third generation SR sources. In fact, undulator radiation has very specific properties that cannot be described in terms of Gaussian-Schell model.
In the present paper we base our theory on the characterization of the cross-spectral density of the system. The cross-spectral density is merely the statistical correlation function of the radiation field at two different positions on the observation plane at a given frequency

bracket indicating an average over an ensemble of pulses. Based on cross-spectral density we developed a comprehensive theory of third generation SR sources in the space-frequency domain, where we exploited the presence of small or large parameters intrinsic in the description of the system.
First, we took advantage of the particular but important situation of perfect resonance, when the field from the undulator source can be presented in terms of laser-like beams described by analytical functions. A cross-spectral density can then be given at the virtual source position, and subsequently propagated anywhere. Second, we exploited the practical case of a Gaussian electron beam, allowing further analytical simplifications. Third, we took advantage of the large horizontal emittance (compared with the radiation wavelength) of the electron beam, allowing separate treatments of horizontal and vertical directions.
In general, the cross-spectral density function in the vertical direction at the virtual source turns out to be a simple convolution of an universal function S (see Fig. 2)
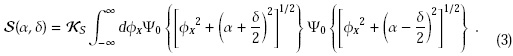
and Gaussian functions:
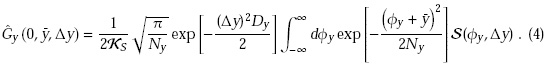
The normalization constant  is chosen in such a way that
is chosen in such a way that 
 with
with  and
and  the size and divergence of the electron bunch in the vertical direction. Eq. (4) can be easily propagated in free-space. We studied asymptotic cases of our theory for third generation light sources with their region of applicability. In particular, we considered both asymptotes of a small and a large vertical emittance compared with the radiation wavelength. In the case of a small vertical emittance the radiation is not diffraction limited in the vertical direction, an effect that can be ascribed to the influence of the large horizontal emittance on the vertical coherence properties of radiation. In the case of a large vertical emittance we described the quasi-homogeneous source in terms of a non-Gaussian model, which has higher accuracy and wider region of applicability with respect to a simpler Gaussian model.
the size and divergence of the electron bunch in the vertical direction. Eq. (4) can be easily propagated in free-space. We studied asymptotic cases of our theory for third generation light sources with their region of applicability. In particular, we considered both asymptotes of a small and a large vertical emittance compared with the radiation wavelength. In the case of a small vertical emittance the radiation is not diffraction limited in the vertical direction, an effect that can be ascribed to the influence of the large horizontal emittance on the vertical coherence properties of radiation. In the case of a large vertical emittance we described the quasi-homogeneous source in terms of a non-Gaussian model, which has higher accuracy and wider region of applicability with respect to a simpler Gaussian model.
|
References |
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
Contact information |
||||||||||||||||||||||||||
|
Dr. Gianluca Geloni |
||||||||||||||||||||||||||
| Further Information |