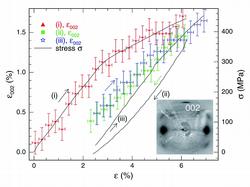
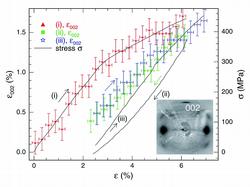
Figure 1: Stress-strain curves of a bundle of silkworm silk fibres (solid lines, right-hand scale). (i) is the initial stretching of a
previously unstretched fibres whereas (ii) and (iii) correspond to the same fibres but pre-stretched (decreasing and increasing strain, respectively). The symbols give the strain of the fibroin crystals (left-hand scale) as determined from the 002 reflections of the fibre diffraction
diagram (inset) measured at HASYLAB Beamline A2. The crystals are deformed by about 25 % of the macroscopic fibre strain, under the assumption of a constant-stress scenario (see also Fig. 2).
Igor Krasnov1, Imke Diddens1,4, Nadine Hauptmann1, Gesa Helms1, Malte Ogurreck1, Tilo Seydel2, Sérgio S. Funari3, Martin Müller1,5
1Institut für Experimentelle und Angewandte Physik, Christian-Albrechts-Universität zu Kiel, 24098 Kiel, Germany
2Institut Laue-Langevin, BP 156, 38042 Grenoble Cedex 9, France
3HASYLAB at DESY, Notkestr. 85, 22607 Hamburg, Germany
4Present address: Oxford Silk Group, Department of Zoology, Oxford University, Oxford, OX1 3PS, UK
5Present address: GKSS Forschungszentrum Geesthacht GmbH, Max-Planck-Straße 1, 21502 Geesthacht, Germany
Published as: “Mechanical Properties of Silk: Interplay of Deformation on Macroscopic and Molecular Length Scales”, Phys. Rev. Lett. 100, 048104, (2008)
Using an in situ combination of tensile tests and X-ray diffraction, we have determined the mechanical properties of both the crystalline and the disordered phase of the biological nanocomposite silk by adapting a model from linear viscoelastic theory to the semicrystalline morphology of silk. We observe a strong interplay between morphology and mechanical properties. Silk‘s high extensibility results principally from the disordered phase; however, the crystals are also elastically deformed.
Silkworm silk is a natural composite material produced by silkworms (Bombyx mori) and has been in use by human for several
thousands of years, mainly for textiles with a silky shine and with excellent thermal insulation properties. Similar to spider silk, silkworm silk has a tensile strength comparable to that of steel. But, unlike steel, it is also extremely stretchable allowing for extreme elongation before breaking and possessing a high degree of toughness with the specific fracture energy much larger than of a high-tensile steel. It would be highly desirable to mimic nature’s spinning process to produce artificial fibres with optimized mechanical performance either from silkworm
or recombinant spider silk spinning dope.
The response of silk to an external force has a very dynamic nature and shows a rich spectrum of relaxation times from the fractions of a second through many hours up to days. This nonstatic nature of the response together with the very specific morphology of silk is the key to its extraordinary mechanical property. Morphologically, spider and silkworm silk are hierarchically structured nanocomposite materials consisting of fibres containing ordered regions (β-sheet protein nanocrystals) embedded in a softer matrix of disordered material. Tensile
deformation of silk fibres involves a strong contribution of viscoelastic material, presumably in the disordered regions.
We carried out two kind of complementary experiments to establish a model for silk incorporating the macroscopic mechanical behaviour, in particular, viscoelasticity, on the basis of its semicrystalline morphology. To this end, we combined high-resolution cyclic stress-strain measurements of single silkworm silk fibres with in situ tensile tests during synchrotron radiation X-ray diffraction experiments, the latter probing directly the deformation of the nanocrystals.
Silkworm silk was investigated at ambient humidity content in all experiments. The stretching measurements on single fibres were carried out with a piezo stretching device equipped with a force sensor. Force and distance were sampled with 1000 s-1. The triangular strain excitation signal is a stepwise realization of a constant rate of strain change 0.1 %/s. The stress-response function was measured for increasing and decreasing strain on a previously unstretched fibre (2.0 mm initial length) and then again in a second cycle for the same, thus, pre-stretched sample.
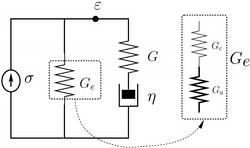
Figure 2: Dashpot-spring representation of the standard three-parameter Maxwell model of a solid. The purely elastic contribution (modulus Ge) may be split up in amorphous and crystalline contribution in serial arrangement (constant stress; Ga and Gc, respectively). The viscoelastic contribution (G and viscosity η) is from the amorphous regions only. All parameters could be determined quantitatively in the in situ X-ray diffraction experiment.
X-ray diffraction experiments were carried out in situ during a stretching experiment on fibre bundles of silkworm silk required for a good signal-to-noise ratio. Synchrotron radiation X-rays were used at Beamline A2, HASYLAB. Fibre diffraction patterns were recorded on a two-dimensional CCD detector. The lattice strain of the β-sheet fibroin crystals in the direction of the tensile stress was determined from the shift of the radial position of the 002 reflection (Fig. 1).
Unlike the unstretched fiber, the pre-stretched sample can be considered to be in a metastable state, because at the time scale of our experiments (which is of the order of seconds to minutes) no changes are observed. However, it returns to the unstretched state after a few days, recovering its initial length and stress-strain behaviour. Most surprisingly, the pre-stretched sample shows a behaviour which allows a very simple phenomenological description in the context of linear viscoelastic theory. The measured data can be well described with the simplest
rheological model, the standard three-parameter Maxwell model of a solid (Fig. 2).
The model parameters are independent of the sample shape and of the time-dependence of the strain excitation. They have to be interpreted as average macroscopic material properties. Known model parameters give us access to values such as elastic modulus, relaxation time, viscosity of the material as whole. However, the model does not allow separating the characteristics of the crystalline phase from those of the amorphous one. In situ X-ray diffraction provides unique access to such individual quantitative information on the crystalline phase as it probes the lattice deformation of the fibroin crystals under tensile load. This delivers a value for the elastic modulus of the crystalline phase and thus allows us to calculate the respective parameter of the amorphous part.
In conclusion, we clearly separated the mechanical properties of the crystalline and the amorphous phase, as well as their interplay, of silk. A link between the macroscopic viscoelastic behaviour and the mechanisms at the molecular length scale has been established. The β-sheet crystals do not only act as nodes in a disordered molecular network [1], but they are elastically deformed themselves and thus contribute to the extensibility of silk. Our new model is purely rheological and does not require any geometrical information (or assumptions) on the distribution of crystalline and amorphous phases, which an analysis in the framework of composite mechanics would do [2]. The model fully accounts for the semicrystalline morphology of silk and is also able to explain the mechanical properties of pre-stretched spider dragline silk, as we confirmed in a fit of data in [3].
|
References |
||||||
|
||||||
|
Contact information |
||||||
|
Martin Müller |
||||||
| Further Information |