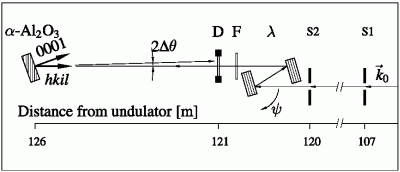
Figure 1: Experimental setup for measuring lattice parameters: X-rays after a high-heat-load monochromator (not shown) are collimated by passing through the vertical slits S1 and S2; λ: λ-meter; F: 57Fe foil used as a source of Mössbauer radiation; D: semi-transparent avalanche photo-diode with 0.7 ns time resolution; α-Al2O3: sapphire single crystal in a LHe flow cryostat on a 4-circle goniometer.
M. Luchta, M. Lerchea, H.-C. Willeb, Yu. V. Shvyd'koa, H. D. Rütera, E. Gerdaua, P. Beckerc
aUniversität Hamburg, Institut für Experimentalphysik, Luruper Chaussee 149, 22761 Hamburg, Germany
bEuropean Synchrotron Radiation Facility, BP220, 38043 Grenoble Cedex, France
cPhysikalisch-Technische Bundesanstalt, Bundesallee 100, 38116 Braunschweig, Germany
Published in: J. Appl. Cryst. 36, part 4, 1075-1081 (2003)
The lattice parameters of sapphire (α-Al2O3) have been measured in a temperature range from 4.5K to 250K with a relative accuracy of better than 6 x 10-6. Sapphire is a potential new material for X-ray crystal optics, especially attractive in applications as Bragg back-scattering mirrors since it allows unlike silicon exact Bragg back-scattering with high reflectivity for X-rays in the 10-50 keV spectral range. However, lattice parameters reported in the literature differ by up to 10-4. This has imposed large uncertainties in the prediction of the back-reflections and the relevant crystal temperatures.
Introduction
Lattice parameters of sapphire (α-Al2O3) single crystals are measured in the temperature range from 4.5K to 250K. The experimental method uses Bragg back-scattering and the recently proposed Mössbauer wavelength standard, i.e. the wavelength λM=86.025474(16)pm of the nuclear resonance radiation of 57Fe [16], which have previously been applied successfully to measure laatice parameters of α-Al2O3 at temperatures between 286K and 374K [17]. The experimental data in the range from 4.5K to 374K are consistent with the Debye model of thermal expansion. At 4.5K the thermal expansion is as low as 1.2 (0.9) x 10-10 K-1 in direction of the a-axis. Sapphire is a potential new material for X-ray crystal optics, especially attractive in applications as Bragg back-scattering mirrors for interferometers, high-energy resolution monochromators, and analyzers, since it allows (unlike silicon) exact Bragg back-scattering with high reflectivity for X-rays in the 10-50keV spectral range [13,15,14].
Precise values of the sapphire lattice parameters and their temperature dependences are required to select suitable back-reflections and relevant crystal temperatures for desired X-ray energies. However, lattice parameters and thermal expansion data for α-Al2O3 reported in the literature [9,4,1,10,20,5] differ by up to 10-4. This imposes large uncertainties in the prediction of the back-reflections and the relevant crystal temperatures. To ensure more precise predictions, the lattice parameters of α-Al2O3 are measured in this work with a relative uncertainty of less than 6x10-6 , extending our previous results for temperatures between 286K and 374K [17].
The temperature region below 250K is of special interest for X-ray back-scattering because - compared to room temperature and above - the thermal expansion of α-Al2O3 is lower, leading to less strict requirements in stability of the temperature control for the crystals which are used as X-ray optical elements. This is especially important for X-ray energies above ≈30keV.
Also the thermal conductivity of α-Al2O3 rises at low temperature, making α-Al2O3 a potential material for high-heat-load monochromators for synchrotron radiation. The thermal conductivity measured in α-Al2O3 is up to 200W cm-1K-1 around 30K [19], which is higher than the thermal conductivity of any other mono-crystalline material suitable for X-ray optics. This may become important at the synchrotron radiation facilities of the fourth generation (XFEL, LCLS), since such sources will provide a beam intensity and heat load that is several orders of magnitude higher compared with today's facilities.
Method
The experimental technique exploits the fact that the wavelength λ of the radiation back-reflected from the atomic planes with Miller indices (hkl) of a crystal is related to the inter-planar distance dhkl by Bragg's law λ=2dhklsinθ. For back-scattering it simplifies to λ=2dhkl(1-Δθ2/2) with Δθ=π/2-θ as angular deviation from exact back-scattering. If 
, where is the required relative accuracy of measurements, the simple relation λ=2dhkl is valid even for a relatively coarse angular adjustment.
The lattice parameters are derived from measurements of the wavelength of the X-rays reflected under the exact back-scattering condition. For this purpose a silicon channel-cut crystal, the so-called λ-meter, is used in the experiment. The symmetric Bragg reflection (777) is applied. By rotating the λ-meter the wavelength of the transmitted radiation is changed. This instrument is calibrated in units of the wavelength λM of the Mössbauer radiation of 57Fe [16] during the experiment.
The experimental setup is shown in Fig. 1. The method is discussed in detail in [17]. In the following four Miller indices are used to denote the atomic planes of α-Al2O3 in the hexagonal basis, where h+k+i = 0. The rotation angle ψhkil where the λ-meter selects the X-rays matching the backscattering reflection is
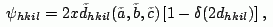
(1)
where 
is the inter-planar distance and 
are the lattice parameters in α-Al2O3; and x=λM/2d*, with d* the inter-planar distance of the reflecting atomic planes in the λ-meter, corrected by refraction and non-perfect angular alignment. Variables notated with a tilde are in units of λM while others are in SI units.
The reference rotation angle where the λ-meter selects the Mössbauer radiation from the 57Fe foil is
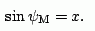
(2)
The combination of Eqs. 1 and 2 leads to the following expression which is used to evaluate the inter-planar distances:
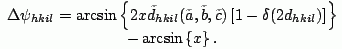
(3)
Herein, 
.
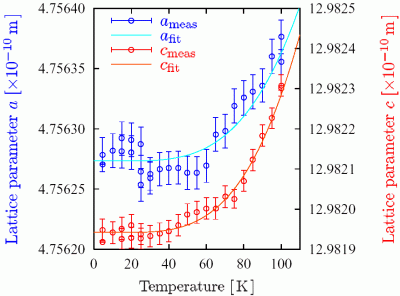
With a=b in the hexagonal α-Al2O3 lattice, there are three unknowns 
to be determined in the experiment. Thus at least three measurements of Δψhkil for different back-reflections (hkil) are required. The measurements are repeated at temperatures of the α-Al2O3 of 250K,200K,150K,100K , and 4.5K.
This method allows direct measurement of the lattice parameters a and c in units of λM. In the range from 100K to 4.5K a technique of relative measurements was used additionally.
Experimental
The experiment was performed at the low energy branch of the undulator beamline at the PETRA II storage ring at HASYLAB/DESY (Germany) [6,7].
Figure 1 shows the experimental setup. The crystal under study is placed on a 4-circle goniometer. It can be oriented to allow for back-reflections of X-rays transmitted by the λ-meter (λ). The back-reflections 
, 
, 
, 
are used in the experiment. They are selected by their Bragg wavelength 
being in the proximity of λM.
The crystal is kept in a liquid helium flow cryostat. By temperature controlled electric heating, it is possible to maintain the crystal at a fixed temperature with a stability of some mK [11]. The λ-meter crystal is kept at a constant temperature (303.8K) with a stability of ≈10mK. It is mounted on a high-resolution angular rotation stage.
If the wavelength of the radiation picked out by the λ-meter coincides with λM, it excites coherently the 57Fe nuclei in an α-Fe foil (F) installed in the beam. The excited nuclei emit Mössbauer photons with coherent enhancement in the forward direction [8,18], with an average delay of τ=141ns. This delay allows for discrimination of the Mössbauer quanta from the synchrotron radiation pulse.
The detector, a semi-transparent silicon avalanche photo-diode [3], with a time resolution of ≅0.7ns, is placed immediately after the λ-meter at a distance L≈6m upstream from the back-scattering crystal. The transmitted radiation is reflected from the α-Al2O3 crystal and arrives after 2L/c =40ns in the detector, which makes the reflected pulse easily distinguishable from the incident pulse.
Data evaluation and results
Sapphire can be assigned to the hexagonal crystal system with two independent lattice parameters a = b and c. The inter-planar distance in a hexagonal lattice is given by:
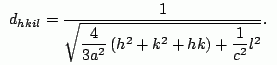
(4)
For each crystal temperature, the angular differences Δψhkil have been measured for the four different back-reflections. This allows us to compose four different sets, each with three equations of type Eq. 3, yielding its own solution for the three free parameters a, c, and d* of the problem. An iteration procedure is used to solve these nonlinear systems of equations.
From the four independent solutions, the averaged values of a and c and their standard errors can be computed.
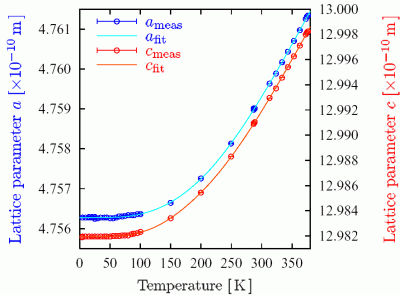
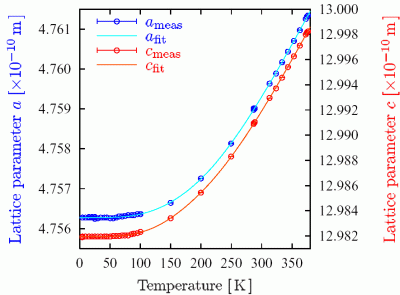
The lattice parameters of α-Al2O3 in the temperature range from 4.5K to 374K , including our recently published results for temperatures above 286K [17], are shown in Fig. 2. For the computation of the lattice parameters in SI units the value λM=86.025474(16)pm from [16] was used. The errors of ã and 
, which are relatively below 6 x 10-6, are primarily due to the averaging process, as described above.
Discussion
In the Debye model of thermal expansion, the linear expansion coefficient α has a T3 dependence for T → 0, and is constant for 
(where 
is the Debye temperature), see e.g. [2]. We have fitted the following function that resembles this behavior to the data of the present work and of [17]:
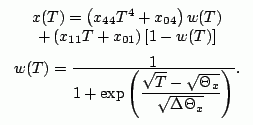
(5)
Herein, x takes the values a or c, respectively. The polynomial terms in parentheses represent the limiting temperature dependence of α as described above, and w(T) and 1 - w(T) are weighting factors that provide a smooth transition around the temperature θx between the T → 0 and T → ∞ regions. Since the weighting factor of the low temperature term extends far into the range above θx, the Debye temperature is expected to be 
. The Debye temperature can be estimated to be 995K for the sub-lattice of O atoms, and 890K for the Al sub-lattice, cf. [13], p.63.
From Eq.5 one can now calculate the linear thermal expansion coefficients for the limiting cases of low and high temperature:
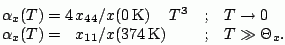
(6)
The value 374K in the second line in Eq. 6 is the maximum temperature used in the determination of the fit.
The fit curves are shown in Fig. 2 together with the measured results for a and c. The relative accuracy of the fit is about 4 x 10-6 which is close to the measurement uncertainty at low temperature. Therefore, it seems evident that possible relative deviations from the Debye model are below 4 x 10-6.
From Eqs. 6 we obtain the following approximate expressions for the thermal expansion coefficients in the limiting cases:
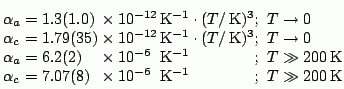
(7)
Conclusions
In the present work and [17], the lattice parameters of α-Al2O3 have been measured in the temperature range from 4.5K to 374K with relative errors below 4 x 10-6. A data fit shows that our results are, within a relative accuracy of about 6 x 10-6, compatible with the Debye model of thermal expansion, where the thermal expansion coefficient shows T3 dependence for T → 0 and is constant for higher temperatures 
.
The accuracy of the present study is more than one order of magnitude below the expected 10-7 which is a theoretical limit of the experimental technique. The main error sources are the large divergence of the incoming beam and crystal defects in α-Al2O3, but also temperature shifts inside the experimental station during the measurements.
The present results will be useful for predicting Bragg back-reflections and relevant crystal temperatures which are needed for a high-resolution α-Al2O3 back-scattering monochromator. Two cases can be distinguished:
i) For temperatures above ≈50K it is possible to tune the back-scattering monochromator to any given X-ray energy between 10 and 50keV. This is done by selection of a back-reflection (hkil) with 2dhkil close to the desired X-ray wavelength λ, and adjustment of the temperature.
ii) For temperatures below ≈40K the relative change of the lattice parameters of α-Al2O3 is not more than 6 x 10-6. This leads to a set of fixed wavelengths λhkil of back-reflected X-rays which are stable even for a rather coarse temperature accuracy and high heat load.
| References |
|
[1] P. Aldebert and J.P. Traverse. J. AM Ceram. Soc., 65:460-464, 1982. |
| Contact information |
|
Martin Lucht |
| Further Information |
