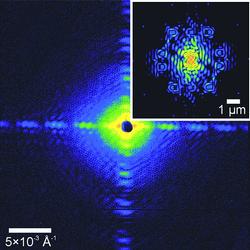
Figure 1: Recorded hologram of a gold nanostructure – the capital letter P – surrounded by 5 reference scatterers. The inset shows the central part of the modulus of the Fourier transform of the recorded diffraction intensities, imaging the object and its rotated copy 5 times each. Logarithmic pseudocolour scale each.

L.-M. Stadler1, C. Gutt1, T. Autenrieth1, O. Leupold1, S. Rehbein2, Y. Chushkin3, G. Grübel1
1 HASYLAB at DESY, 22607 Hamburg, Germany
2 BESSY, 12489 Berlin, Germany
3 ESRF, 38043 Grenoble, France
Published as: “Hard X-Ray Holographic Diffraction Imaging”, Phys. Rev. Lett. 100, 245503 (2008)
Nanoscience mandates the ability to characterise the structure of objects on the nanoscale. For several reasons, hard X-rays are very attractive for that purpose: a wavelength in the order of ≈1 Å allows for excellent spatial resolution; the high penetration into matter permits to study thick samples or even buried structures in an easy-to-realise experimental setup; and with the upcoming hard X-ray free-electron lasers the achievable time resolution will be pushed down to the femtosecond (fs) regime. Here, we demonstrate how coherent hard X-rays can be used for a determination of the absolute electron density of a lithographically tailored gold nanostructure (the letter P) from a single diffraction experiment, yielding both the shape and the height of the sample. We combine Fourier transform holography (FTH) [1], which – by a single Fourier transform – gives an unambiguous image of the sample structure, with iterative phase retrieval procedures known in the field of coherent diffraction imaging (CDI) [2]. The latter enable us to push the spatial resolution toward the diffraction limit, which is determined by the maximum photon momentum transfer.
In FTH phase retrieval becomes particularly simple, since in a typical setup the object and a spatially nearby reference are coherently illuminated and a single Fourier transform of the recorded hologram yields the convolution of the object and reference amplitudes, where the spatial resolution achievable is comparable to the reference source size [1,3]. Provided the sampling of the diffraction pattern is sufficiently high [4], the FTH result can be used as starting point for further iterative phase retrieval in order to increase the resolution. In the present case 5 gold dots with about 175 nm diameter were placed on a circle of 2.5 μm radius around the gold nanostructure, each acting as reference source in the scattering process.
The corresponding hologram, which is shown in Fig. 1, was recorded at the ESRF beamline ID10C using coherent 8 keV photons. The hologram is the sum of 200 single pictures each exposed 3s. That is the hologram has been recorded with 1010 photons. A single Fourier transform of the measured intensities gives the spatial autocorrelation of the overall object, including the cross-correlation between the object and the dots, which directly yields the object shape and its complex conjugate (a 180°-rotated copy) for each dot, as can be seen in Fig. 1.
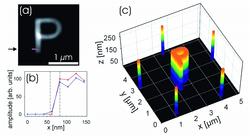
The letter P is clearly recognizable, its shape is, however, slightly distorted and the contrast is reduced by the wavy background. This image degradation stems from the pixels blocked by the beamstop. In addition the big reference source size causes a blurring of the P structure in the FTH reconstruction. For further progress the individual images are averaged for improving statistics and the result – already comprising a qualitative image of the object – is fed into iterative CDI algorithms [2]. Carrying out such phase retrieval runs yielded an image of the sample’s electron density projected along the beam direction with ≈25 nm resolution (see Fig. 2b). Knowing that the sample under investigation was made of gold and exploiting the fact that the scattering process can be described as Thomson scattering, it is straight forward to derive a mean sample height, which would be the correct height if the sample were flat.
Figure 2: Results from the FTH-based phase retrieval runs. (a) Average amplitude of 100 phase retrieval runs. (b) Slices through an individual run demonstrating a resolution of 25 nm. (c) The overall object geometry.
Actually, in the present case we can, in fact, tell how well the assumption of a flat sample topography is, since this information is encoded in the phases of the hologram’s Fourier transform. This allowed us to obtain the phase profile of the sample and by taking Fresnel diffraction effects [5] into account we could deduce the corresponding height profile. For our sample we find a homogeneous height of approximately 235 nm. The final reconstruction yielded the overall object geometry and height as shown in Fig. 2.
In conclusion, we have shown that hard X-ray holographic diffraction imaging is an excellent technique for determining electron density profiles on the nanoscale. Using the FTH result as input facilitates the following iterative phase retrieval dramatically and the spatial resolution can be pushed toward the diffraction limit. By virtue of this concept we determined the absolute electron density and derived both shape and height of a lithographic gold nanostructure. The presented approach with coherent hard X-rays is ideally suited for applications in materials science, where samples can be thick, may consist of buried structures, or have to be measured under extreme conditions such as high pressure. Finally, we envision experiments of similar type to be carried out at future hard X-ray free-electron laser sources, where diffraction patterns can be collected within a single shot at the time scale of ≈10 fs, opening fascinating possibilities for imaging fast dynamic processes.
|
References |
||||||||||
|
||||||||||
|
Contact information |
||||||||||
|
Christian Gutt |
||||||||||
| Further Information |