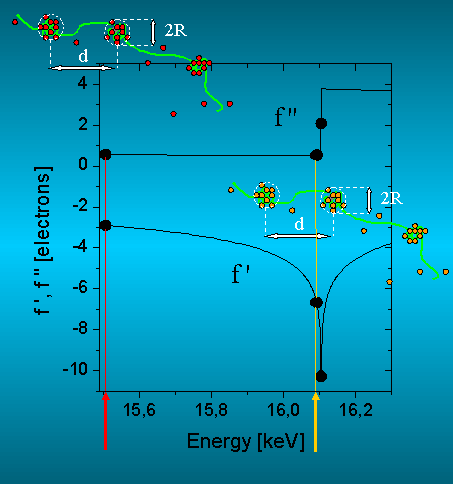
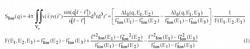Figure 2: Anomalous dispersion corrections of Strontium in the energy range of the K-absorption edge at 16.105 keV. The scattering contribution of the Sr-counterions change strongly with the energy, while the scattering contribution of the polymer filament remains nearly constant. The different colours of the pearl-like structures denote the different scattering contrast.
G. Goerigk1, R. Schweins2 and K. Huber3
1Institut für Festkörperforschung, Forschungszentrum Jülich, Postfach 1913, D-52425, Germany
2Institut Laue-Langevin, Large Scale Structures Group, B.P. 156, F-38042 Grenoble CEDEX 9, France
3Universität Paderborn, Fakultät für Naturwissenschaften, Department Chemie, Warburger Str. 100, D-33098 Paderborn, Germany
Published in: Europhys. Lett., 66 (3), pp. 331-337 (2004)
Polyelectrolytes are highly charged macromolecules. A large variety of such systems, where the role of electric charge is essential for the structure and proper functioning has been discovered in nature like for instance nucleic acids, numerous enzymes or self assembling proteins. Due to the high charge density, concentrated on the chain, polyelectrolytes show a strong interaction between the segments of the same chain and other macromolecules as well as they exhibit a characteristic counterion condensation around their charges. This in turn influences the conformational properties of the chains. Determination of the counterion distribution may thus help to better understand folding properties of polyelectrolytes and their specific functioning. The counterion distribution was analyzed by Anomalous Small-Angle X-ray Scattering (ASAXS).
Anomalous small-angle X-ray scattering (ASAXS) with synchrotron radiation is a suitable experimental technique, which allows the structural characterization of the counterion distribution around the macroions by tuning the energy in the vicinity of the absorption edge of the ion in question. The distribution of the counterions is not accessible by conventional SAXS measurements, because the scattering contributions of the counterions and the macroions superimpose and cannot be distinguished. The first ASAXS results of counterion distributions were reported by Stuhrmann [1]. The results of the present contribution are published in [2].
|
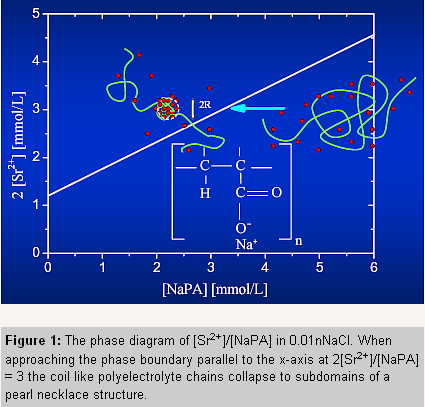
The present contribution deals with the conformation of the sodium salt of polyacrylic acid (NaPA) in aqueous solutions with 0.01 M NaCl and pH 9. NaCl was added in order to screen the electrostatic interaction between polyelectrolyte chains. In contradiction to Na+, Sr2+ binds specifically and more tightly to the carboxylate groups. This interaction neutralizes the polyanions to a large extent, and due to the hydrophobic nature of the backbone, leads to a collapse of the polyelectrolyte chains [5]. Theoretical work on this shrinking process, based on scaling arguments and Monte Carlo simulations propose that polyeclectrolyte structure passes elongated intermediates like cigars or pearl necklaces [3,4] before reaching the spherical shape. However, these conformations have not yet been observed experimentally. If a large fraction of the carboxylate sites is occupied by Sr2+ ions, the spacial distribution of the Sr2+ ions should reflect the monomer density distribution within the collapsing chain and anomalous small angle X-ray scattering (ASAXS) is a well-suited experimental technique to study the correlation of the macroion with its counterions [1,2]. |
Sample preparation |
ASAXS measurements were performed at the JUSIFA beamline [6] at HASYLAB, DESY Hamburg in the range of the K-absorption edge of Strontium at 16.105 keV. The energy dependence of the small angle X-ray scattering near the K-absorption edge of Sr is used to access directly by analytical means the pure-resonant scattering contribution of the Sr-ions by measuring the small-angle scattering at only three suitable energies (Figure 2). In Figures 3 and 4 the scattering curves of P4KE and P4KU2 are shown. The squares show the total scattering curves comprising both, polymer chains and counterions measured at the energy 15.507 keV. The triangles show the separated (mixed- and pure resonant) scattering, which corresponds to the superposition of the scattering from the polyacrylates and the Sr-counterions. The separated scattering curves were obtained from measurements at the two energies 15.507 and 16.105 keV and the separation was performed due to eq.(4) in [2]. The circles represent the formfactors of the distributions of the Sr-counter ions. These formfactors were obtained from measurements at the three energies 15.507, 16.093 and 16.105 keV (Figure 2) due to eq. (1) [2].
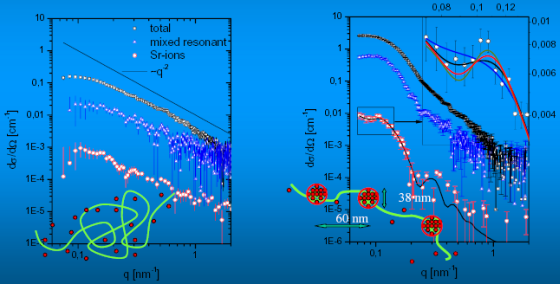
In Figure 3 the scattering curves of NaPA-chains at [NaPA]=3.61 mM (P4KE) obtained from SAXS measurements are shown. The total as well as the separated (mixed-resonsant) scattering curve and the formfactor of the distribution of Sr-counterions follow a power law of dσ/dΩ~q-α. The exponent α is close to 2 for the three curves, indicating a coil like behavior [7].
The scattering curves (total, separated and formfactor of Sr-ion-distribution) of the second sample (P4KU2) with a smaller concentration of NaPA ([NaPA] = 3.25 mM), but the same SrCl2 content as P4KE in Figure 4 show a different behavior. The total scattering curve is contracted to smaller q-values and shows several shoulders. This behavior is compatible with the formfactor of spherical objects, which is modulated by inter-spherical scattering contributions. This interpretation is strongly confirmed by the separated scattering curve (triangles) and the formfactor of the pure-resonant scattering curve (circles), which represents the scattering of the Sr-ion distribution. Both curves exhibit a number of characteristic structures for q > 0.1 nm-1 with pronounced maxima, minima and shoulders revealing a scattering function, which is strongly influenced by correlation effects between rather monodisperse subdomains within the collapsing chains.
Especially the formfactor of the spatial distribution of the Sr-counter ions reveals a correlation maximum at 0.1 nm-1. The solid line in Figure 4 represents a fitted model function to the formfactor of the Sr-ion distribution. For a counterion condensation-induced shrinking process such a model was first suggested by Rubinstein et al. [3] and was confirmed later by computer simulations [4,8-9]. The model, denoted as pearl-necklace, gives the scattering function of N spheres with radius R0 and with a distance d between the spheres. For the size distribution of the spheres a log-normal size distribution P(R) was assumed (Eq. 2):
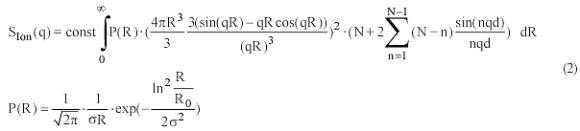
σ is the second moment of the log-normal size distribution. The first bracket in the integral contains the formfactor of a single sphere multiplicated with the correlations (second bracket) introduced by the interference of the scattering from the N spheres. An increase of the number of spheres N at constant d (i) increases the overall size of the pearl necklace; (ii) has small but siginificant effects in the regime of 0.06nm-1<q<0.12nm-1 where a minimum and a maximum occurs (inset of Figure 4); (iii) does not significantly affect the three fit parameters σ, d and R0 ; (iv) does not affect the scattering curve for q>0.14nm-1. The maximum appears only for N>3. Although eq. (2) accounts for a polydispersity, the model is still rather crude due to the assumption of a regular sphere-like structure for the pearls and due to neglect of a polydispersity of the pearl size within each necklace chain respectively.
However in the light of these trends and simplifications, we kept the fit as simple as possible, predifining the number of pearls at N=3. As a result we found: R0 = 19 nm for the mean radius of the spheres, σ = 0.088 for the second moment of the log-normal size distribution, which corresponds to a FWHM in the size distribution of 4 nm and finally d = 60 nm for the distance of the spheres. In this interpretation the fitted model function points into the direction of scattering originating from more than two pearls (dumb-bell).
| References |
|
[1] H B. Stuhrmann, Advances in Polymer Science 67, 123-163 (1985) |
| Contact information |
|
Günter Goerigk |