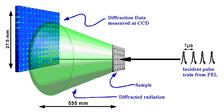
Figure 1: A sketch of the experiment. The beam from the beamline first interacts with the sample, and then the diffracted radiation propagates to a CCD detector. To enhance the measured resolution of the data the direct beam was incident near the corner of the detector (Zoom: detailed version).
A.P. Mancuso1, A. Schropp1, B. Reime1, L.-M. Stadler1, A. Singer1, J. Gulden1, S. Streit-Nierobisch1,C.Gutt1, G. Grübel1, J. Feldhaus1, F. Staier2, R. Barth2, A. Rosenhahn2, M. Grunze2, T. Nisius3, T. Wilhein3, D. Stickler4, H. Stillrich4, R. Frömter4, H.P. Oepen4, M. Martins5, B. Pfau6, C.M. Günther6, R. Könnecke6, S. Eisebitt6, B. Faatz1, N. Guerassimova1, K. Honkavaara1, V. Kocharyan1, R. Treusch1, E. Saldin1, S. Schreiber1, E.A. Schneidmiller1, M.V. Yurkov1, E. Weckert1, and I.A. Vartanyants1
1 HASYLAB at DESY, 22607 Hamburg, Germany
2 Angewandte Physikalische Chemie, Universität Heidelberg, Im Neuenheimer Feld 253, D-69120 Heidelberg, Germany
3 Institute for X-ray-Optics, RheinAhr-Campus Remagen, FH Koblenz, Südallee 2, D-53424 Remagen, Germany
4 Institut für Angewandte Physik, Universität Hamburg, Jungiusstraße 11, D-20355 Hamburg, Germany
5 Institut für Experimentalphysik, Universität Hamburg, Luruper Chaussee 149, D-22761 Hamburg, Germany
6 Berliner Elektronenspeicherring-Gesellschaft für Synchrotronstrahlung m.b.H. (BESSY), Albert-Einstein-Straße 15, D-12489 Berlin, Germany
Published as: ''Coherent-pulse 2D Crystallography at Free Electron Lasers'' Phys. Rev. Lett. 102, 035502/1-5 (2009).
Crystallization and radiation damage is presently a bottleneck in protein structure determination. We propose to use two-dimensional (2D) finite crystals and ultrashort Free Electron Laser pulses to reveal the structure of single molecules. This can be especially important for membrane proteins that in general do not form 3D crystals, but easily form 2D crystalline structures. We have demonstrated single pulse train coherent diffractive imaging for a finite 2D crystalline sample, and conclude that this alternative approach to single molecule imaging is a significant step towards revealing the structure of proteins with sub-nanometer resolution at the newly built XFEL sources.
Revealing the structure of protein molecules is mandatory for understanding the structure of larger biological complexes. The major progress in uncovering the structure of proteins in past decades was due to the development of phasing methods [1] allowing the determination of the structure of complex molecules that crystallize. One new approach to overcome these difficulties is based on the use of ultrashort pulses of x-ray free-electron lasers (XFEL) [2]. This elegant idea is based on measuring a sufficiently sampled diffraction pattern from a single molecule illuminated by an FEL pulse [3]. However, in spite of the extreme intensity of the FEL pulses, a diffraction pattern from only one molecule will not be sufficient to obtain a high resolution diffraction pattern. Many reproducible copies will need to be measured to get a sufficient signal to noise ratio for each projection necessary for three-dimensional (3D) imaging at sub-nanometer spatial resolution.
Free-electron lasers are especially well suited for such coherent 2D crystallography. They provide femtosecond coherent pulses with extremely high power. Only the combination of all of these unique properties will allow the realization of 2D crystallographic x-ray imaging on biological systems. Brilliant, ultrashort pulses could overcome the radiation damage problem [3] which is a severe limitation of conventional crystallography at 3rd generation synchrotron sources [4]. Higher luminosity and hence improved statistics for such experiments can be obtained by the use of pulse trains that can be provided by FLASH [5].
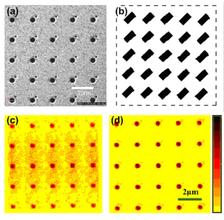
We demonstrate finite crystallography by using a micro-structured crystal array that was prepared on a 100 nm thick silicon nitride membrane substrate coated with 600 nm of gold, and 200 nm of palladium. The finite crystal sample was manufactured by milling holes in the film in a regular array pattern using a Focused Ion Beam (FIB). The 'unit cell' of our crystal consists of a large hole of 500 nm diameter (representing a 'heavy atom' in conventional crystallography) and a smaller hole of 200 nm diameter (representing a 'light atom'). The whole structure is composed of five unit cells in each direction, making the total structure size about 10 μm x 10 μm.
The diffraction data were measured at FLASH on the PG2 monochromator beamline [6] with a fundamental wavelength of 7.97 nm. The scheme of experiment is shown in Fig. 1.
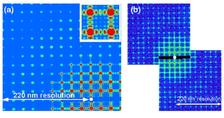
We used a 0.2 s exposure time to collect a series of single pulse train data from our sample with a coherent flux on the sample area of 1.5x1010 photons per pulse train. This is an order of magnitude higher than the expected coherent flux of about 3x109 photons on the same sample area for the same exposure time at a 3rd generation synchrotron source. A typical data set is shown in Fig. 2(a). The diffraction pattern as measured contains signal up to the edge of the detector, which corresponds to a minimum feature size of 220 nm (Fig. 2(a)). We note that all expected features of a finite, crystalline structure are observed. The Bragg peaks due to the regular array are clearly seen, as are the oscillations between the Bragg peaks that are the result of the finite extent and coherent illumination of our sample. Also seen is the form factor from the individual elements – the large holes – that can be observed as a radial intensity modulation across the pattern produced.
The preprocessed data set (shown in Fig. 2(b)) was used for reconstruction by applying the Hybrid Input-Output (HIO) iterative phase retrieval algorithm [7]. A scanning ion micrograph (SIM) image of the object under investigation is shown in Fig. 3(a). The initial square support used for reconstruction is indicated by a dashed line in Fig. 3(b). It is very clearly seen in Fig. 3(c) that the periodic array of large holes are successfully reconstructed, however the small holes of 200 nm diameter are missing. Note also the diffuse, elongated background present in the reconstruction.
Our analysis have shown that one of the reasons for the limited resolution and its sensitivity to noise obtained in our initial reconstructions is due to the fact that the measured diffraction pattern has two equivalent, symmetric solutions. One is with the small dots appearing to the top right of the larger dots, and the other is with them appearing to the bottom left. Due to this symmetry the reconstruction algorithm does not fully converge, but rather stagnates with two equivalent solutions superimposed with each other. To solve this problem we have binned the data 5x5 (yielding a sampling rate of 6 in each dimension). In addition, instead of using a large square support we use a more constrained support of 25 rectangular boxes each centered on the positions of the unit cell (see Fig. 3(b)). By improving the signal-to-noise ratio and reducing the symmetry in real space we were able to improve the reconstruction to the level that we resolved the smallest features present in our sample (Fig. 3(d)). Our analysis has shown that obtained resolution in real space was better than 238 nm. This compares favorably with our measured maximum momentum transfer that corresponds to 220 nm resolution (see Fig. 2).
In summary we have demonstrated single pulse train coherent diffractive imaging for a finite crystalline sample with the reconstructed image exhibiting resolution commensurate with the maximum momentum transfer measured in the diffraction data. Furthermore, we demonstrate that the traditionally non-crystalline framework of coherent diffractive imaging is applicable to two-dimensional finite crystals. In this experiment the 2D crystalline structure has been essential in providing the necessary signal to determine the structure of the unit cells. If only a single unit cell were used simulations suggest that a successful reconstruction to the resolution shown here would be impossible. These findings improve the scope of the fast growing technique of coherent imaging by including finite 2D crystalline specimens in the sphere of applicability of CXDI, and by utilizing these crystals to improve signal to noise, and hence resolution of CXDI reconstructed images. We conclude that this alternative approach to single molecule imaging is a significant step towards revealing the structure of proteins with sub-nanometer resolution at the newly built XFEL sources.
| References | ||||||||||||||
|
| Contact Information |
|
Ivan Vartaniants |
| Further Information |