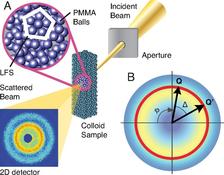
Figure 1: Sketch of the experimental setup where a speckle diffraction pattern is generated in the far field when coherent X-rays illuminate a disordered sample. a) illustrates the local icosahedral symmetry of the arrangement of PMMA balls in the colloidal sample and b) outlines the XCCA analysis method.
Peter Wochner1, Christian Gutt2, Tina Autenrieth2, Thomas Demmer1, Volodymyr Bugaev1, Alejandro Díaz Ortiz1, Agnès Duri2, Federico Zontone3, Gerhard Grübel2, Helmut Dosch1,2
1. Max-Planck-Institut für Metallforschung, Heisenbergstrasse 3, D-70569 Stuttgart, Germany.
2. DESY, Notkestrasse 85, D-22607 Hamburg, Germany.
3. European Synchrotron Radiation Facility, 6 rue Jules Horowitz BP 220, 38043 Grenoble Cedex 09, France.
Published as: “X-ray cross correlation analysis uncovers hidden symmetries in disordered matter”, Proceedings of the National Academy of Sciences 106, 11511-11514 (2009).
The different local symmetries in colloidal glasses were investigated by coherent X-ray scattering beyond the standard pair correlation analysis. By analyzing the resulting speckle patterns with a newly developed X-ray cross correlation analysis (XCCA) concept, it is possible to access and classify the otherwise hidden local order within disorder. Four-, six-, ten- and, most prevailing, five-fold symmetries are observed coupled to distinct momentum transfer (Q) values, which do not coincide with the maxima of the amorphous structure factor. The observation of dynamical evolution of these symmetries forms a connection to dynamical heterogeneities in glasses. The XCCA concept opens up a fascinating view into the world of disorder and will definitely allow, with the advent of free-electron X-ray lasers, an accurate and systematic experimental characterization of the structure of the liquid and glass states.
Disordered matter, such as glasses and liquids, does not exhibit translational symmetry and in turn is able to accommodate different local symmetries in the same system, among them the icosahedral local order, which belongs to the forbidden motifs in periodic structures. This mysterious and so far experimentally inaccessible localized order within disorder has been fascinating scientists for many decades [1-3], as it is held responsible for the under-cooling of liquids and the existence of the glass state. Yet, it has been frustratingly difficult to characterize it quantitatively, since commonly used tools such as X-ray and neutron scattering, which are capable of probing structure at atomic dimensions in bulk materials, yield only orientationally averaged information embodied in the so-called “radial pair distribution function” which simply tells you the average number of particles at a certain distance from a given particle. Without a periodic crystal lattice, the elegant methods of conventional crystallography cannot be applied. This limitation can be overcome if coherent light is scattered, like in a snapshot, from the instantaneous positions of all the atoms in the disordered sample. In this case a speckle pattern is generated in the far field due to the interference of radiation coming from the entire scattering volume and the (not completely) random phase shifts by the particles [4]. A speckle pattern represents a unique fingerprint via Fourier transform of the individual sample, rather than the usual ensemble average accessed by scattering with standard incoherent radiation [5].
An example of a speckle pattern is shown in Fig. 1 together with a sketch of the experiment. In this study, highly concentrated glassy suspensions of sterically stabilised PMMA particles were investigated by coherent X-ray scattering at beamline ID10A of the ESRF with a similar experimental setup as for XPCS [6]. The envelope of the fluctuating speckle intensities is in fact the ensemble-averaged S(Q) scattering function that is normally measured from a glass or liquid as shown in Fig. 2a. S(Q) depends only on pair-correlations and for amorphous samples does not depend on bond angles. To extract information on the local ordering hidden in the speckle pattern, the instantaneous scattered intensity was analysed for angular correlations by calculating a 4-point correlation function
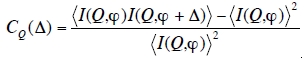
where Δ is the azimuthal angle difference between two points in the speckle pattern (see Fig. 1b). The averaging indicated by the brackets is taken over the entire ring φ∈[0;2π] with |Q|=Q. Most fascinating is that CQ(Δ) in Fig. 2b clearly reveals a very pronounced anisotropy with 5-fold symmetry specifically for the intensity ring associated with Q=0.04 nm-1, which points to a so far hidden local symmetry in the colloidal system. The different Q-dependent symmetries are a signature of the specific local order. The colloidal glasses investigated here are slowly evolving; hence the analysis could be performed over time intervals much shorter than the typical speckle decay time (~200s) to yield the temporal evolution of the local ordering. It is found that the bond-orientational order symmetries slowly relax as a function of time and switch e.g. from 5-fold to 6-fold at a given Q value. This is qualitatively related to the structural rearrangement of local entities or clusters that could be the cages in the so-called alpha relaxation [7]. The emerging picture is that clusters of icosahedral order reorganize themselves and are formed either in nanocrystalline environments or out of complete disorder, all of which involves the breaking and formation of bonds. This bears similarities to the behaviour observed in simulations of supercooled molecular liquid glass-formers and underlines the importance of local rearrangements in the understanding of the dynamical properties of this important class of non-periodic materials [8]. Clearly, there is a wealth of new information about the kinetics and the origin of the glass transition to be mined from such experiments, by e.g. applying correlators testing for medium range order. The application of these techniques to metallic glasses and liquids require scattering experiments at much shorter length scales and thus higher Q values, where even at the current high-brilliance synchrotron X-ray sources, one is fighting battles against both intensity and the degree of coherence of the X-ray beam, particularly for liquids where one would have to take fast snap-shot pictures of the speckle patterns. The availability of short-pulse XFEL radiation in the 0.1-nm regime and with sub 100-fs pulse length will open up the fascinating option to analyze the local structure of liquids (in particular also water) by applying the new concept of X-ray cross correlation analysis (XCCA) to single laser shot speckle diffraction pattern. This single shot technique is also suited to study nanopowders and transient complex molecular structures in solutions via a pump-probe scheme.
| References | ||||||||||||||||
|
| Contact information |
|
Peter Wochner |
| Further Information |