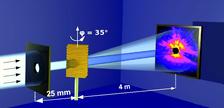
Figure 1: Schematic view of the CXDI experiment showing the pinhole, the sample and the detector.
J. Gulden1, O. M. Yefanov1, A. P. Mancuso1, V. V. Abramova2, J. Hilhorst2, D. Byelov2, I. Snigireva3, A. Snigirev3, A. V. Petukhov3, I. A. Vartanyants1
1. Deutsches Electronen-Synchrotron (DESY), Notkestraße 85, D-22607 Hamburg, Germany
2. Van't Hoff Laboratory for Physical and Colloid Chemistry, Debye Institute, University of Utrecht, Padualaan 8, 3508 TB Utrecht, The Netherlands
3. ESRF, 6 rue Jules Horowitz, F-38043 Grenoble, France
Published as: “Coherent x-ray imaging of defects in colloidal crystals’’, Phys. Rev. B Vol. 81, 224105 (2010).
Real crystalline materials, in contrast to the idealized model of a perfect crystal, contain a broad spectrum of defects. These defects determine most of the mechanical, optical and electronic properties of the crystals. Visualization of the defect core in a bulk material with X-ray methods still remains a challenge. Here we demonstrate how to use coherent X-ray diffractive imaging (CXDI) to map such defects in colloidal crystals. The inversion of the diffraction patterns reveals the arrangement of colloidal particles in a face-centered cubic (fcc) lattice as well as defects in the form of stacking faults in the (111) planes.
Self-organized colloidal crystals are an attractive material for modern technological devices. They can be used as the basis for novel functional materials such as photonic crystals, which may find applications in future solar cells, LEDs, lasers or even as the basis for circuits in optical computing and communication. For these applications crystal quality is crucial and monitoring the defect structure of real colloidal crystals is essential [1].
The experiment was performed at the microoptics test bench at the ID06 beamline of the European Synchrotron Radiation Facility (ESRF) with an incident X-ray energy of 14 keV. The geometry of the experiment (Fig. 1) allows for rotation of the sample around the vertical axis perpendicular to the incident X-ray direction. A 7 μm pinhole was positioned at a close distance in front of the colloidal crystal. This pinhole selects a highly coherent part of the beam and produces a finite illumination area. The initial orientation of the sample (with azimuthal angle φ = 0°) corresponds to the direction of the incident X-rays along the [111] direction of the fcc colloidal crystal and was perpendicular to the surface normal of the sample. Rotating the sample around the vertical axis allows the measurement of different sets of diffraction planes. Particularly important was the direction of the incident X-rays along the [110] direction of the colloidal sample lattice at φ = 35°, when the set of (111) planes was aligned along the incident beam. The diffraction data were recorded by using a CCD detector with 4005 · 2671 pixels with a resolution of Δq = 0.16 μm-1 per pixel. In the experiment a thin film of a colloidal crystalline sample on a glass substrate was used. It was grown by the convective assembly technique using polystyrene microspheres (diameter 425 nm, relative standard deviation <5%). The grown crystalline films have a face-centered cubic (fcc) structure and were typically 20 to 30 layers thick.
Positioning the sample just after the aperture yields strong fringes typical of an Airy pattern [2] from a circular aperture, centered at q = 0 (Fig. 2a,d). In addition, due to the long range order in the colloidal crystal, several orders of Bragg peaks are easily visible in the diffraction pattern. Strongest is the hexagonal set of 220 Bragg peaks typical for scattering from a fcc structure. Each of these Bragg peaks contains a few orders of diffraction fringes similar to those at q = 0, due to the finite aperture in front of the sample. In addition to the allowed 220 Bragg peaks, we also observed much weaker forbidden peaks (⅓ (224) in our case). Their appearance is an indication of defects in the crystal.
A real space image of a colloidal sample obtained by applying the guided hybrid input-output algorithm [3] to a processed diffraction pattern, shown in Fig. 2b, is presented in Fig. 2c. This image represents a projection of the ‘atomic’ structure of the colloidal crystal along the [111] direction. The hexagonal structure is clearly visible across the whole illuminated region, with only slightly lower intensity values of the image around the edges of the pinhole aperture. An estimate of the resolution gives a value of 95 nm (FWHM) at the particle positions in Fig. 2c.
The diffraction patterns, measured at an angle of φ = 35° (Fig. 2d), were especially intriguing. They show strong streaks of varying intensity originating at the Bragg peaks with an angle of 55° ( Figs. 2d,e) to the horizontal direction. It is well known from previous studies [4] of similar colloidal systems that such streaks in reciprocal space are induced by stacking faults in the fcc structure in the (111) planes. The result of the phase retrieval of the processed diffraction pattern shown in Fig. 2e is presented in Fig. 2f. The ‘atomicity’ of the colloidal crystal sample is again present in the reconstruction. In addition, a stacking fault (indicated by arrows in Fig. 2f) appears as a break in the ‘correct’ ABC ordering [5]. One can see a stacking fault, which consists of two hcp planes, and two fcc domains with the same stacking direction. The effect of the stacking fault here is a translation of the two fcc crystals relative to each other.
We demonstrated here that the simple and non-destructive mechanism of coherent X-ray diffractive imaging opens a unique route to determine the structure of mesoscopic materials such as colloidal crystals. CXDI has the potential to provide detailed information about the local defect structure in colloidal crystals. This is especially important for imaging photonic materials when refraction index matching is not possible or the sizes of colloidal particles are too small for conventional optical microscopy. To extend this method to larger fields of view scanning methods such as ptychography [6] can be used, while tomographic methods such as coherent X-ray tomography [7] have the potential to visualize the atomic structure of the defect core in 3D.
| References | ||||||||||||||
|
| Contact information |
|
Ivan Vartaniants |
| Further Information |