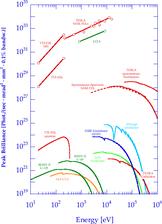
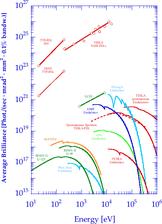
Figure 6: Peak brilliance of XFELs and undulators for spontaneous radiation at TESLA and at the LCLS, Stanford [17], in comparison to the undulators at present third generation synchrotron radiation sources. In addition, also the spontaneous spectrum of an XFEL undulator is shown.
In the following part the originally planned TESLA XFEL is described, which was proposed in 1997. The basic technology underlying the FLASH and European XFEL facility is a superconducting linac - the TESLA technology, developed by DESY and international partners.
Information from 2006:
As already mentioned, the characteristics of FEL radiation are high power, short pulse length, narrow bandwidth, spatial coherence and wavelength tunability.
In this section, some examples will be given that shed light on the differences between the TESLA XFELs and state-of-the-art synchrotron radiation sources to illustrate the exceptional properties of an FEL. Table 1 gives an example of some typical photon beam parameters for one of the planned XFELs at TESLA (a detailed discussion of the properties of all XFEL undulators at TESLA can be found in the TDR Part V, Chap. 4).
|
Units |
SASE1 |
|
|---|---|---|
|
Wavelength* |
Å |
1-5 |
|
Peak power |
GW |
37 |
|
Average power |
W |
210 |
|
Photon beam size (FWHM)** |
µm |
100 |
|
Photon beam divergence (FWHM)*** |
µrad |
0.8 |
|
Bandwidth (FWHM) |
% |
0.08 |
|
Coherence time |
fs |
0.3 |
|
Pulse duration (FWHM) |
fs |
100 |
|
Min. pulse separation**** |
ns |
93 |
|
Max. number of pulses per train**** |
# |
11500 |
|
Repetition rate**** |
Hz |
5 |
|
Number of photons per pulse |
# |
1.8 x 1012 |
|
Average flux of photons |
#/sec |
1.0 x 1017 |
|
Peak brilliance |
B***** |
8.7 x 1033 |
|
Average brilliance |
B***** |
4.9 x 1025 |
*Parameters are given for the shortest wavelength.
** Value at the exit of the undulator.
*** Far field divergence.
**** Values determined by the time structure of the electron beam in the accelerator. The average parameters for the SASE-1 FEL are given for the ultimate case when only this beamline is in operation.
***** In units of photons/( sec · mrad2 · mm2 · 0.1%bandwidth).
One of the key parameters to compare different radiation sources is their brilliance3. For partially coherent light sources (wigglers and undulators) the brilliance
[photons/( sec · mrad2 · mm2 · 0.1%bandwidth)] can be calculated from the spectral flux
[photons/( sec · 0.1%bandwidth)] divided by the photon beam's rms radius ∑ and divergence ∑' obtained from convolution of the electron beam and photon diffraction parameters as
|
|
(5) |
|
|
|
(6) |
|
|
|
(7) |
|
|
In the case of full transverse coherence (e.g. FELs in saturation) ∑ and ∑ are related through |
||
|
|
(8) |
|
|
and Equation (5) can be transformed into |
||
|
|
(9) |
|
|
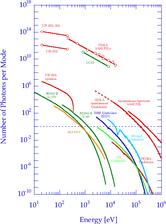
This means that the brilliance is simply given by the spectral flux divided by the transverse photon phase space. |
||
|
|
(10) |
|
Eight orders of magnitude more photons per mode reflect the improved coherence of the FELs compared to the spontaneous emission of third generation SR sources. In summary, extremely short pulses, high intensity and full transverse coherence are the attractive features of the FEL radiation.
3 Note: In the US the European "brilliance" is mostly called "brightness". "Spectral brightness" is currently the preferred unit in the community.
(see: Report of the Working Group on Synchrotron Radiation Nomenclature – brightness, spectral brightness or brilliance? J. Synchrotron Rad. (2005). 12, 385)