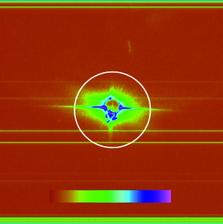
Figure 1: Top: SEM image of ellipsoidal iron oxide nanoparticles. Bottom left: Example diffraction pattern with saturation and aperture scatter. Bottom right: pre-processed diffraction pattern with high q values and saturated regions removed that are assembled with cryptotomography.
N. D. Loh1,11, M. J. Bogan2, V. Elser1, A. Barty3, S. Boutet2, S. Bajt4, J. Hajdu5, T. Ekeberg5, F. R. N. C. Maia5, J. Schulz3, M. M. Seibert5, B. Iwan5, N. Timneanu5, S. Marchesini6, I. Schlichting7,8, R. L. Shoeman7,8, L. Lomb7,8, M. Frank9, M. Liang3, H. N. Chapman3,10
1. Laboratory of Atomic and Solid State Physics Cornell University, Ithaca, New York 14853-2501, USA
2. SLAC National Accelerator Laboratory, 2575 Sand Hill Road, Menlo Park, California 94025, USA
3. Center for Free-Electron Laser Science, DESY, Notkestrasse 85, Hamburg 22607, Germany
4. Photon Science, DESY, Notkestrasse 85, Hamburg 22607, Germany
5. Laboratory of Molecular Biophysics, Department of Cell and Molecular Biology, Uppsala University, Husargatan 3, Box 596, SE-75124 Uppsala, Sweden
6. Lawrence Berkeley National Laboratory, 1 Cyclotron Road, Berkeley, California 94720, USA
7. Max Planck Institute for Medical Research, Jahnstraße 29, 69120 Heidelberg, Germany
8. Max Planck Advanced Study Group, Center for Free-Electron Laser Science, DESY, Notkestrasse 85, Hamburg 22607, Germany
9. Lawrence Livermore National Laboratory, 7000 East Avenue, Livermore, California 94550, USA
10. University of Hamburg, Luruper Chaussee 149, Hamburg 22761, Germany
11. Cornell High Energy Synchrotron Source (CHESS), Cornell University, Ithaca, New York 14853-2501, USA
Published as: “Cryptotomography: Reconstructing 3D Fourier Intensities from Randomly Oriented Single-Shot Diffraction Patterns”, Phys. Rev. Lett. 104, 239902 (2010).
A new method called cryptotomography combines two dimensional (2D) diffraction patterns of identical particles, each collected in a random and unknown orientation, to unravel the full three-dimensional (3D) image of the average particle. We carried out the first demonstration of cryptotomography by collecting diffraction patterns of ellipsoidal iron oxide nanoparticles at FLASH. These particles were shot across the FEL beam, in vacuum, using the techniques being developed for single-molecule imaging. This demonstration is an important step towards the 3D imaging of noisy and weakly scattering biological samples at X-ray free electron laser sources.
The ultrafast pulses from X-ray FELs open up a new avenue to high-resolution structure determination [1]. By using pulses shorter than the timescale of radiation damage, we can beat the limits imposed by the degradation of the sample in the beam. This gives the potential to image objects that are too small or too radiation sensitive to be studied using conventional synchrotron methods, including viruses and macromolecules that cannot be crystallised. At FLASH, we have demonstrated that the high-resolution imaging methodology of crystallography can be applied to single shot imaging of non-periodic objects. The images obtained by phase retrieval in this “diffraction before destruction” method show no evidence of radiation damage [2]. In general, a full 3D image requires obtaining information from many views of a sample, mapping out the 3D distribution of Fourier intensities. However, unlike crystallography or tomography, where an object can be rotated in order to map out this information, “diffraction before destruction” requires a serial stream of identical objects to acquire the 3D information.
As it is difficult to manipulate or determine the orientations of very small particles, they are injected into the FEL radiation at random, unmeasured orientations. Nevertheless, sufficiently many 2D diffraction patterns from an ensemble of identical albeit randomly oriented particles can in principle overdetermine the particle’s band-limited 3D Fourier intensities. Many schemes have been proposed to combine these patterns in the correct orientation with respect to each other, but these methods require strong signals and low noise. Cryptotomography, implemented with an expansion-maximization-compression (EMC) procedure, was specifically developed by Elser and Loh to combine patterns of weak signal and significant noise [3].
For our proof-of-principle experiments, iron oxide nanoparticles were injected into the FLASH beam using a nebulizer to create an aerosol that was subsequently focused by an aerodynamic lens stack [4]. The 7 nm wavelength FLASH beam ran at a 100 kHz bunch repetition rate, with bunches at 5 Hz. One-second exposures were acquired, and the data obtained showed aperture scatter, saturation, and variation of intensity due to fluctuation of the pulse energy. Preprocessing of the data included truncation of high frequencies, removal of saturated pixel values, and background subtraction. From a large dataset, 54 suitably preprocessed diffraction patterns were chosen to be assembled using cryptotomography.
Our algorithm for recovering the particle’s 3D intensities is based on expectation maximization [5]. This procedure uses a rule to maximize the log likelihood function of the Poisson distribution of the intensities at each pixel. The model intensities determined are the set of 3D intensities and fluences most statistically compatible with the set of diffraction patterns. In the current work, the probability of three parameters are maximized – the intensity, orientation, and fluence. Maximization of all parameters for all the diffraction patterns requires an iterative procedure called the EMC procedure. First the model is expanded into a set of diffraction tomograms (expansion). Then a new model, which maximizes the likelihood that the data corresponds to tomograms of the model, is determined (maximization). Finally, to ensure that the tomograms are consistent with a single model, the interpolated intensities are averaged for all the tomograms (compression). This new model is then reinserted into the EMC algorithm for another iteration.
A random 3D array of Fourier intensities was the initial model. The model was expanded into 3240 tomograms and the algorithm yielded an ellipsoidal particle with dimensions along the principle axes of 30.5 ± 0.8 nm, 30.6 ± 0.7 nm, and 76.1 ± 1.1 nm from R-factor comparisons with an ideal ellipsoid. In addition, fluence probabilities for the 54 diffraction patterns were determined. Iterative phase retrieval was not performed on this particular dataset due to pixilation effects but in principle a real-space image can be determined.
Our result is the precursor for the assembly of more complex structures, in particular due to the ability of the algorithm to handle noisy and sparse data with diffraction patterns obtained at varying fluences. The robustness of the algorithm will be important, as smaller biological samples will have limited contrast and thus suffer from weak signal. The success of this technique with non-optimal data is a step towards 3D diffractive imaging of reproducible samples at X-ray FEL sources.
| References | ||||||||||
|
| Contact information |
|
Mengning Liang |
| Contact information |